Function describing the standard deviation of the measurement error in dependence of the measured value \(y\):
Details
$$\sigma = \sqrt{ \sigma_{low}^2 + y^2 * {rsd}_{high}^2}$$ sigma = sqrt(sigma_low^2 + y^2 * rsd_high^2)
This is the error model used for example by Werner et al. (1978). The model proposed by Rocke and Lorenzato (1995) can be written in this form as well, but assumes approximate lognormal distribution of errors for high values of y.
References
Werner, Mario, Brooks, Samuel H., and Knott, Lancaster B. (1978) Additive, Multiplicative, and Mixed Analytical Errors. Clinical Chemistry 24(11), 1895-1898.
Rocke, David M. and Lorenzato, Stefan (1995) A two-component model for measurement error in analytical chemistry. Technometrics 37(2), 176-184.
Ranke J and Meinecke S (2019) Error Models for the Kinetic Evaluation of Chemical Degradation Data. Environments 6(12) 124 doi:10.3390/environments6120124 .
Examples
times <- c(0, 1, 3, 7, 14, 28, 60, 90, 120)
d_pred <- data.frame(time = times, parent = 100 * exp(- 0.03 * times))
set.seed(123456)
d_syn <- add_err(d_pred, function(y) sigma_twocomp(y, 1, 0.07),
reps = 2, n = 1)[[1]]
f_nls <- nls(value ~ SSasymp(time, 0, parent_0, lrc), data = d_syn,
start = list(parent_0 = 100, lrc = -3))
library(nlme)
f_gnls <- gnls(value ~ SSasymp(time, 0, parent_0, lrc),
data = d_syn, na.action = na.omit,
start = list(parent_0 = 100, lrc = -3))
if (length(findFunction("varConstProp")) > 0) {
f_gnls_tc <- update(f_gnls, weights = varConstProp())
f_gnls_tc_sf <- update(f_gnls_tc, control = list(sigma = 1))
}
f_mkin <- mkinfit("SFO", d_syn, error_model = "const", quiet = TRUE)
f_mkin_tc <- mkinfit("SFO", d_syn, error_model = "tc", quiet = TRUE)
plot_res(f_mkin_tc, standardized = TRUE)
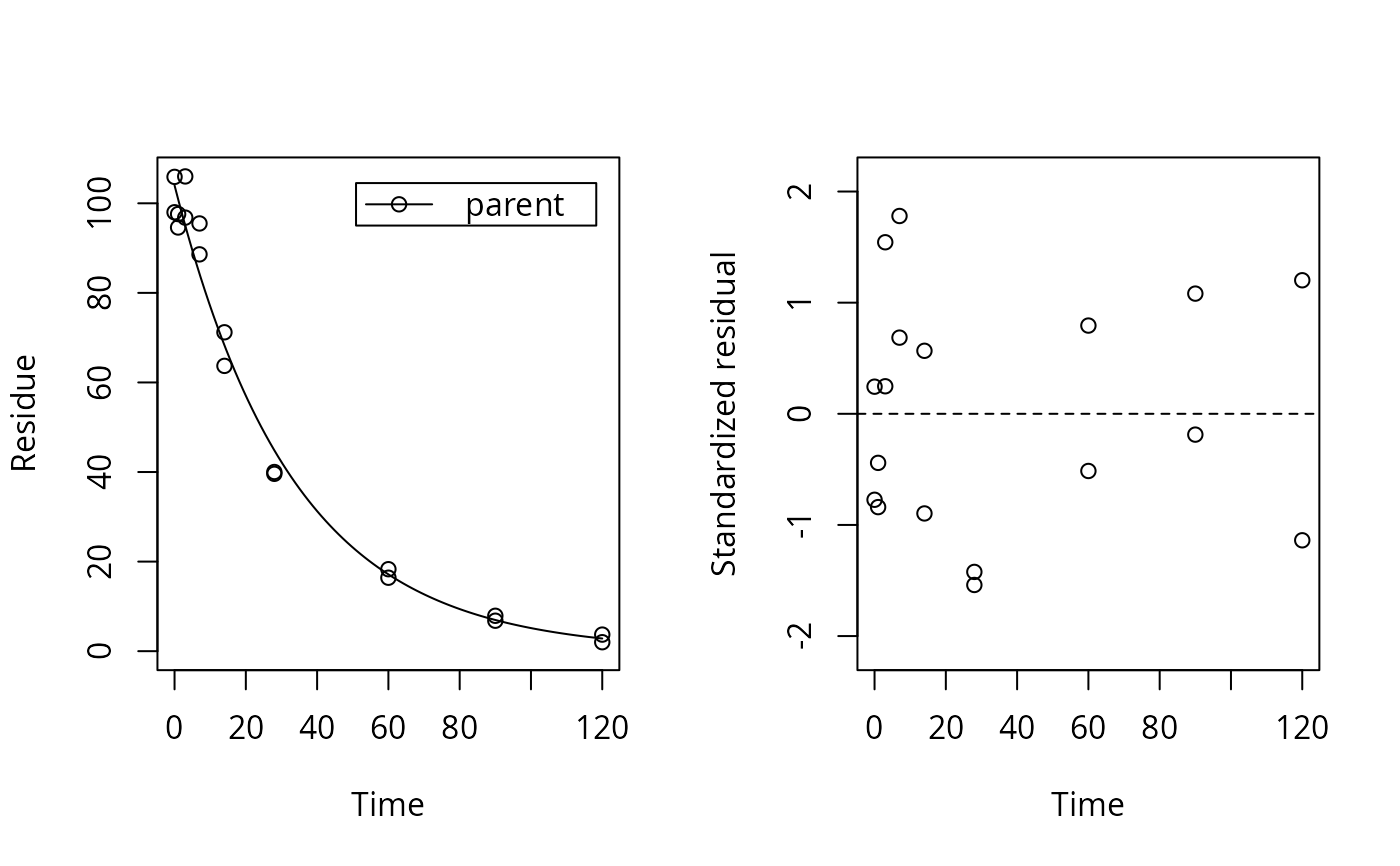 AIC(f_nls, f_gnls, f_gnls_tc, f_gnls_tc_sf, f_mkin, f_mkin_tc)
#> df AIC
#> f_nls 3 114.4817
#> f_gnls 3 114.4817
#> f_gnls_tc 5 103.6447
#> f_gnls_tc_sf 4 101.6447
#> f_mkin 3 114.4817
#> f_mkin_tc 4 101.6446
AIC(f_nls, f_gnls, f_gnls_tc, f_gnls_tc_sf, f_mkin, f_mkin_tc)
#> df AIC
#> f_nls 3 114.4817
#> f_gnls 3 114.4817
#> f_gnls_tc 5 103.6447
#> f_gnls_tc_sf 4 101.6447
#> f_mkin 3 114.4817
#> f_mkin_tc 4 101.6446