Short introduction to mkin
Johannes Ranke
Last change 18 May 2023 (rebuilt 2025-05-12)
Source:vignettes/mkin.rmd
mkin.rmdWissenschaftlicher Berater, Kronacher
Str. 12, 79639 Grenzach-Wyhlen, Germany
Privatdozent at the
University of Freiburg
Abstract
In the regulatory evaluation of chemical substances like plant
protection products (pesticides), biocides and other chemicals,
degradation data play an important role. For the evaluation of pesticide
degradation experiments, detailed guidance has been developed, based on
nonlinear optimisation. The R add-on package
mkin implements fitting some of the models recommended in
this guidance from within R and calculates some statistical measures for
data series within one or more compartments, for parent and
metabolites.
library("mkin", quietly = TRUE)
# Define the kinetic model
m_SFO_SFO_SFO <- mkinmod(parent = mkinsub("SFO", "M1"),
M1 = mkinsub("SFO", "M2"),
M2 = mkinsub("SFO"),
use_of_ff = "max", quiet = TRUE)
# Produce model predictions using some arbitrary parameters
sampling_times = c(0, 1, 3, 7, 14, 28, 60, 90, 120)
d_SFO_SFO_SFO <- mkinpredict(m_SFO_SFO_SFO,
c(k_parent = 0.03,
f_parent_to_M1 = 0.5, k_M1 = log(2)/100,
f_M1_to_M2 = 0.9, k_M2 = log(2)/50),
c(parent = 100, M1 = 0, M2 = 0),
sampling_times)
# Generate a dataset by adding normally distributed errors with
# standard deviation 3, for two replicates at each sampling time
d_SFO_SFO_SFO_err <- add_err(d_SFO_SFO_SFO, reps = 2,
sdfunc = function(x) 3,
n = 1, seed = 123456789 )
# Fit the model to the dataset
f_SFO_SFO_SFO <- mkinfit(m_SFO_SFO_SFO, d_SFO_SFO_SFO_err[[1]], quiet = TRUE)
# Plot the results separately for parent and metabolites
plot_sep(f_SFO_SFO_SFO, lpos = c("topright", "bottomright", "bottomright"))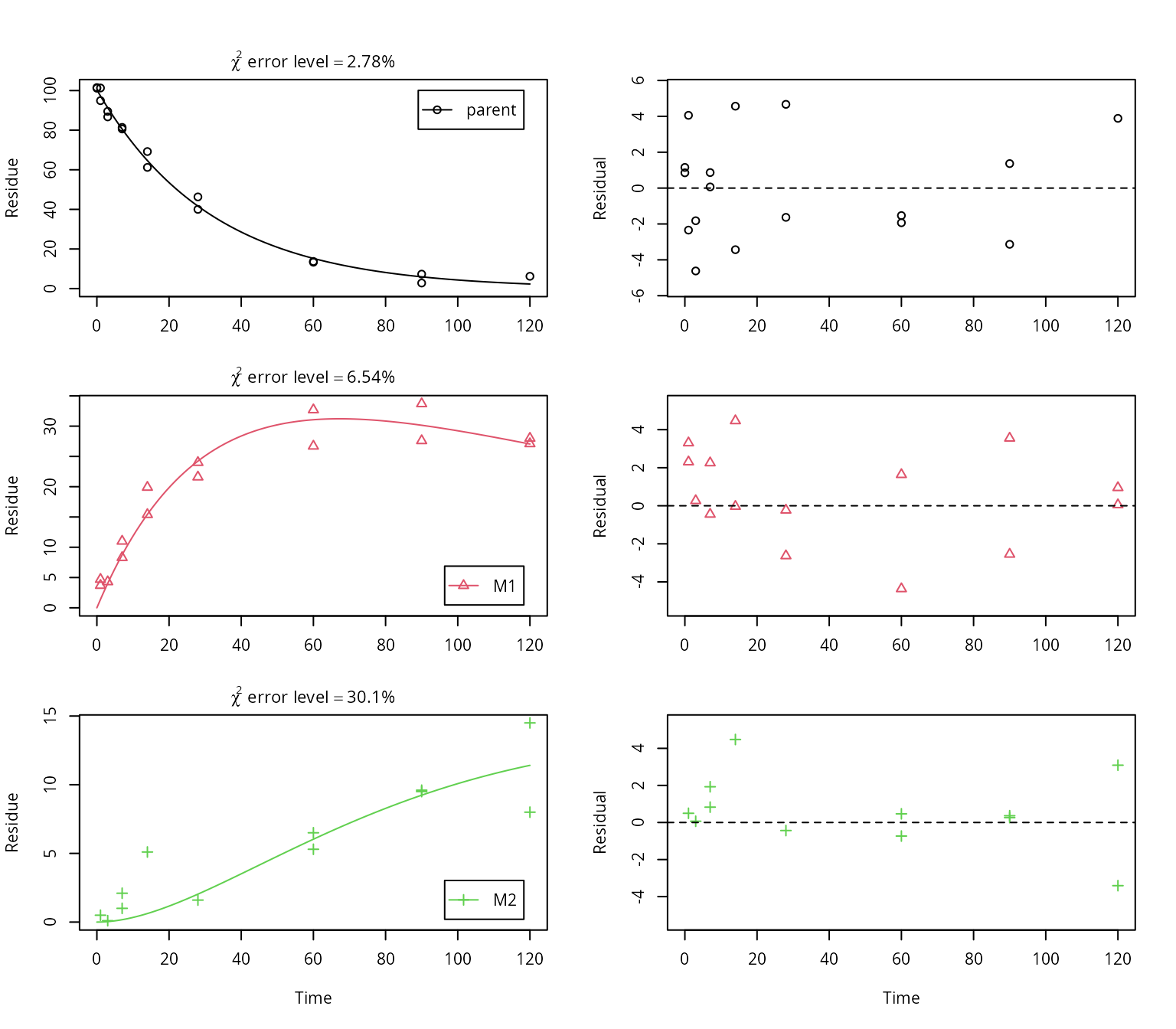
Background
The mkin package (J. Ranke
2021) implements the approach to degradation kinetics recommended
in the kinetics report provided by the FOrum for Co-ordination of
pesticide fate models and their USe (FOCUS Work
Group on Degradation Kinetics 2006, 2014). It covers data series
describing the decline of one compound, data series with transformation
products (commonly termed metabolites) and data series for more than one
compartment. It is possible to include back reactions. Therefore,
equilibrium reactions and equilibrium partitioning can be specified,
although this often leads to an overparameterisation of the model.
When the first mkin code was published in 2010, the most
commonly used tools for fitting more complex kinetic degradation models
to experimental data were KinGUI (Schäfer et al.
2007), a MATLAB based tool with a graphical user interface that
was specifically tailored to the task and included some output as
proposed by the FOCUS Kinetics Workgroup, and ModelMaker, a general
purpose compartment based tool providing infrastructure for fitting
dynamic simulation models based on differential equations to data.
The ‘mkin’ code was first uploaded to the BerliOS development platform. When this was taken down, the version control history was imported into the R-Forge site (see e.g. the initial commit on 11 May 2010), where the code is still being updated.
At that time, the R package FME (Flexible Modelling
Environment) (Soetaert and Petzoldt 2010)
was already available, and provided a good basis for developing a
package specifically tailored to the task. The remaining challenge was
to make it as easy as possible for the users (including the author of
this vignette) to specify the system of differential equations and to
include the output requested by the FOCUS guidance, such as the
error level as defined in this guidance.
Also, mkin introduced using analytical solutions for
parent only kinetics for improved optimization speed. Later, Eigenvalue
based solutions were introduced to mkin for the case of
linear differential equations (i.e. where the FOMC or DFOP
models were not used for the parent compound), greatly improving the
optimization speed for these cases. This, has become somehow obsolete,
as the use of compiled code described below gives even faster execution
times.
The possibility to specify back-reactions and a biphasic model
(SFORB) for metabolites were present in mkin from the very
beginning.
Derived software tools
Soon after the publication of mkin, two derived tools
were published, namely KinGUII (developed at Bayer Crop Science) and
CAKE (commissioned to Tessella by Syngenta), which added a graphical
user interface (GUI), and added fitting by iteratively reweighted least
squares (IRLS) and characterisation of likely parameter distributions by
Markov Chain Monte Carlo (MCMC) sampling.
CAKE focuses on a smooth use experience, sacrificing some flexibility in the model definition, originally allowing only two primary metabolites in parallel. The current version 3.4 of CAKE released in May 2020 uses a scheme for up to six metabolites in a flexible arrangement and supports biphasic modelling of metabolites, but does not support back-reactions (non-instantaneous equilibria).
KinGUI offers an even more flexible widget for specifying complex kinetic models. Back-reactions (non-instantaneous equilibria) were supported early on, but until 2014, only simple first-order models could be specified for transformation products. Starting with KinGUII version 2.1, biphasic modelling of metabolites was also available in KinGUII.
A further graphical user interface (GUI) that has recently been
brought to a decent degree of maturity is the browser based GUI named
gmkin. Please see its documentation page and manual
for further information.
A comparison of scope, usability and numerical results obtained with these tools has been recently been published by Johannes Ranke, Wöltjen, and Meinecke (2018).
Unique features
Currently, the main unique features available in mkin
are
- the speed increase by using compiled code when a compiler is present,
- parallel model fitting on multicore machines using the
mmkinfunction, - the estimation of parameter confidence intervals based on transformed parameters (see below) and
- the possibility to use the two-component error model
The iteratively reweighted least squares fitting of different variances for each variable as introduced by Gao et al. (2011) has been available in mkin since version 0.9-22. With release 0.9.49.5, the IRLS algorithm has been complemented by direct or step-wise maximisation of the likelihood function, which makes it possible not only to fit the variance by variable error model but also a two-component error model inspired by error models developed in analytical chemistry (Johannes Ranke and Meinecke 2019).
Internal parameter transformations
For rate constants, the log transformation is used, as proposed by Bates and Watts (1988, 77, 149). Approximate intervals are constructed for the transformed rate constants (compare Bates and Watts 1988, 135), i.e. for their logarithms. Confidence intervals for the rate constants are then obtained using the appropriate backtransformation using the exponential function.
In the first version of mkin allowing for specifying
models using formation fractions, a home-made reparameterisation was
used in order to ensure that the sum of formation fractions would not
exceed unity.
This method is still used in the current version of KinGUII (v2.1 from April 2014), with a modification that allows for fixing the pathway to sink to zero. CAKE uses penalties in the objective function in order to enforce this constraint.
In 2012, an alternative reparameterisation of the formation fractions was proposed together with René Lehmann (J. Ranke and Lehmann 2012), based on isometric logratio transformation (ILR). The aim was to improve the validity of the linear approximation of the objective function during the parameter estimation procedure as well as in the subsequent calculation of parameter confidence intervals. In the current version of mkin, a logit transformation is used for parameters that are bound between 0 and 1, such as the g parameter of the DFOP model.
Confidence intervals based on transformed parameters
In the first attempt at providing improved parameter confidence
intervals introduced to mkin in 2013, confidence intervals
obtained from FME on the transformed parameters were simply all
backtransformed one by one to yield asymmetric confidence intervals for
the backtransformed parameters.
However, while there is a 1:1 relation between the rate constants in the model and the transformed parameters fitted in the model, the parameters obtained by the isometric logratio transformation are calculated from the set of formation fractions that quantify the paths to each of the compounds formed from a specific parent compound, and no such 1:1 relation exists.
Therefore, parameter confidence intervals for formation fractions obtained with this method only appear valid for the case of a single transformation product, where currently the logit transformation is used for the formation fraction.
The confidence intervals obtained by backtransformation for the cases where a 1:1 relation between transformed and original parameter exist are considered by the author of this vignette to be more accurate than those obtained using a re-estimation of the Hessian matrix after backtransformation, as implemented in the FME package.
Parameter t-test based on untransformed parameters
The standard output of many nonlinear regression software packages includes the results from a test for significant difference from zero for all parameters. Such a test is also recommended to check the validity of rate constants in the FOCUS guidance (FOCUS Work Group on Degradation Kinetics 2014, 96ff).
It has been argued that the precondition for this test, i.e.
normal distribution of the estimator for the parameters, is not
fulfilled in the case of nonlinear regression (J.
Ranke and Lehmann 2015). However, this test is commonly used by
industry, consultants and national authorities in order to decide on the
reliability of parameter estimates, based on the FOCUS guidance
mentioned above. Therefore, the results of this one-sided t-test are
included in the summary output from mkin.
As it is not reasonable to test for significant difference of the
transformed parameters (e.g.
)
from zero, the t-test is calculated based on the model definition before
parameter transformation, i.e. in a similar way as in packages
that do not apply such an internal parameter transformation. A note is
included in the mkin output, pointing to the fact that the
t-test is based on the unjustified assumption of normal distribution of
the parameter estimators.